Глава IV.  Оценка ценных бумаг. Инвестиционные риски

I.  Модели оценки финансовых активов

Финансовый актив, являясь в принципе обычным товаром на рынке капиталов, может быть охарактеризован ценой, стоимостью, доходностью и риском.

Цена финансового актива реально существует и объективна, по крайней мере, в том смысле, что она объявлена и товар по ней равнодоступен любому участнику рынка. Внутренняя стоимость неопределённа и субъективна.

Можно сформулировать несколько условных правил, позволяющих провести определённое различие между ценой и стоимостью финансового актива:

1.     Стоимость - это расчётный показатель, а цена - декларированный, т.е. объявленный, который можно видеть в прейскурантах, ценниках, котировках;

2.     С известной долей условности можно утверждать, что стоимость первична, а цена вторична, так как в условиях рынка цена стихийно устанавливается как среднее из оценок стоимости, рассчитываемых инвесторами;

3.     В любой конкретный момент времени цена однозначна, а стоимость многозначна, так как зависит от числа профессиональных участников рынка.

В зависимости от того, что является методологическим и информационным обеспечением процесса оценивания, существуют три основные теории оценки: фундаменталистическая, технократическая и теория "ходьбы наугад".

Фундаменталисты считают, что любая ценная бумага имеет внутренне присущую ей ценность, которая может быть количественно оценена, как дисконтированная стоимость будущих поступлений, генерируемых этой бумагой, т.е. нужно двигаться от будущего к настоящему. Всё зависит от того, насколько точно удаётся предсказать эти поступления, а это можно сделать, анализируя общую ситуацию на рынке, инвестиционную и дивидендную политику компании, инвестиционные возможности и т.п.

Технократы, напротив, предлагают двигаться от прошлого к настоящему и утверждают, что для управления текущей внутренней стоимостью конкретной ценной бумаги достаточно знать лишь динамику её цены в прошлом. Используя статистику цен, они предлагают  строить различные долго-, средне- и краткосрочные тренды и на их основе определять, соответствует ли текущая цена актива его внутренней стоимости.

Последователи теории "ходьбы наугад" считают, что текущие цены финансовых активов гибко отражают всю релевантную информацию, в том числе и относительно будущего ценных бумаг. Поскольку новая информация с одинаковой степенью вероятности может быть как "хорошей", так и "плохой", невозможно с большей или меньшей определённостью предсказать изменения цены в будущем.

Фундаменталистическая теория является наиболее распространённой. Согласно этой теории, текущая внутренняя стоимость (V_t) может быть рассчитана по формуле:

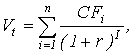                                   (4.1)

где     CFi - ожидаемый денежный поток в i-м периоде;

           r - приемлемая (ожидаемая или требуемая) доходность.

Приемлемая норма прибыли может устанавливаться инвестором следующими способами:

-         в размере процентной ставки по банковским депозитам (r_б);

-         исходя из процента, выплачиваемого банком вкладчику за хранение его средств (r_б) и надбавки за риск инвестирования в данный финансовый актив (r_r):

r=z_b+r_r;

-         исходя из процента, выплачиваемого по правительственным облигациям (r_sb) и надбавки за риск (r_r):

r=r_sb+r_r.

II.  Облигации

Облигации являются долговыми ценными бумагами. Они могут выпускаться  в обращение государством или корпорациями; в последнем случае облигации называются долговыми частными ценными бумагами. Как правило, облигации приносят их владельцам доход в виде фиксированного процента к нарицательной стоимости. Вместе с тем существуют облигации с плавающей ставкой, меняющейся по некоторому вполне определённому алгоритму.

По сроку действия облигации подразделяются на краткосрочные (от года до 3 лет), среднесрочные (от 3 до 7 лет), долгосрочные (от 7 до 30 лет) и бессрочные (выплаты процентов осуществляются неопределённо долго).

По способам выплаты дохода облигации различают:

-         с фиксированной купонной ставкой;

-         с плавающей купонной ставкой (размер процента по облигации зависит от уровня ссудного процента);

-         с равномерно возрастающей купонной ставкой (она может быть увязана с уровнем инфляции);

-         с нулевым купоном (эмиссионный курс облигаций устанавливается ниже номинального, разница между ними представляет собой доход инвестора, выплачиваемый в момент погашения облигации, процент от облигации не выплачивается).

Облигации могут быть охарактеризованы различными стоимостными показателями, основными из которых являются нарицательная (или номинальная), конверсионная, выкупная и рыночная.

Нарицательная стоимость напечатана на самой облигации и используется чаще всего в качестве базы для начисления процентов.

Конверсионная стоимость - расчётный показатель, характеризующий стоимость облигации в условиях эмиссии, которой предусмотрена возможность конверсии её при определённых условиях в обыкновенные акции фирмы-эмитента.

Выкупная цена - это цена, по которой производится выкуп облигации эмитентом, по истечении срока облигационного займа или до этого момента, если такая возможность предусмотрена условиями займа.

Рыночная (курсовая) цена облигации определяется конъюнктурой рынка. Значение рыночной цены облигации в процентах к номиналу называется курсом облигации.

Оценка облигации с нулевым купоном производится по уравнению:

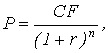                                        (4.2)

где     CF - сумма, выплачиваемая при погашении облигации.

Пример: Облигация с нулевым купоном нарицательной стоимостью 100 тыс. рублей и сроком погашения через 5 лет продаётся за 63012 рублей. Проанализировать целесообразность приобретения этих облигаций, если имеется возможность альтернативного инвестирования с нормой прибыли 12%

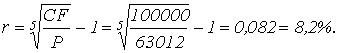
Приобретать не выгодно.

Бессрочная облигация предусматривает неопределённо долгую выплату дохода (CF) в установленном размере или по плавающей процентной ставке. В первом случае формула (4.1) трансформируется в формулу суммы членов бесконечно убывающей геометрической прогрессии, поэтому:

,                                               (4.3)

Пример: Вычислить теоретическую стоимость бессрочной облигации, если выплачиваемый по ней годовой доход составляет 10 тыс. рублей, а рыночная (приемлемая) норма прибыли – 18%

.

Оценка безотзывной облигации с постоянным годовым доходом производится по уравнению:

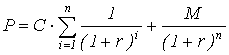,              (4.4).

где         M – номинал облигации;

               C – купонный доход

Пример: Рассчитать рыночную цену облигации нарицательной стоимостью 100 тыс. руб. купонной ставкой 15% годовых и сроком погашения 4 года, если рыночная норма прибыли 10%. Процент по облигации выплачивается дважды в год.

По уравнению (4.4).

Если норма прибыли будет 18%, то

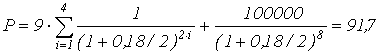 тыс. р.

Приблизительную оценку доходности купонной облигации без права досрочного погашения можно произвести по формуле:

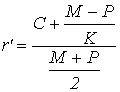,                                                     (4.5)

где         M – номинал облигации;

                P – текущая цена (на момент оценки);

               C – купонный доход;

                K – число лет, оставшихся до погашения облигации.

     Пример. Рассчитать доходность облигации нарицательной стоимостью 100 тыс. руб. с годовой купонной ставкой 9%, имеющей текущую рыночную цену 84 тыс. руб.; облигация будет приниматься к погашению через 8 лет.

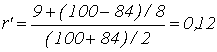 или 12%;

Облигации с правом досрочного погашения в отличие от облигаций без этого права имеют ещё одну характеристику – доходность досрочного погашения (r’’).

Пример: Облигация номиналом 1000 дол. с погашением через 10 лет была выпущена три года назад. В настоящее время её цена равна  1050 дол. Проценты выплачиваются каждые полгода по ставке 14% годовых. В проспекте эмиссии указано, что в течении пяти лет предусмотрена защита от долгосрочного погашения. Выкупная цена превышает номинал на сумму годовых процентов. Рассчитать показатели доходности r’ и r’’.

Для расчётов воспользуемся формулой (4.4)

;

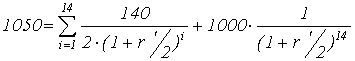отсюда r¹= 12,89%

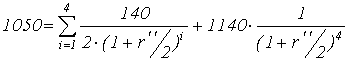
отсюда r^''= 17,1%

Выводы: доходность облигации за прошедшие три года снизились с 14% до 12,89%. Значение r’’ значительно превосходит доходность к погашению, поэтому складывается впечатление, что досрочное погашение выгодно держателям облигаций. Однако такой вывод не вполне корректен. Если ставки будут и далее снижаться, эмитенту станет невыгодно платить повышенный процент по сравнению со средним на рынке. Поэтому компания предпочтёт досрочно погасить облигационный займ и вместо него разместить новый с купонной ставкой 10%.

Для корректности сравнения предполагается, что в случае досрочного погашения держатель, получив выкупную цену, приобретает облигации первого выпуска этого же эмитента, т.е. в расчёте на одну старую облигацию он может вложить 1140 дол. в новый выпуск. Полугодовой доход составит при этом: 57 дол. (потери 13 дол.). Потери за 10 лет  104,4 дол.

При погашении (как предусмотрено условиями эмиссии) он получит 1140 дол. это составит на начало нового 10-летнего периода 86 дол. т.е. он теряет 18,40 дол.

III.  Долевые ценные бумаги

Долевыми ценными бумагами являются различные виды акций. Различают несколько количественных характеристик, используемых для оценки акций: внутренняя, номинальная, балансовая, конверсионная и ликвидационная, а также эмиссионная и курсовая цена.

Внутренняя стоимость представляет собой расчётный показатель, вычисленный, например, по формуле (4.1).

Конверсионную стоимость можно рассчитывать для привилегированных акций, в условиях эмиссии которых, предусмотрена возможность их конверсии в обыкновенные акции.

Номинальная стоимость акции – это стоимость, указанная на бланке акции, характеризующая долю уставного капитала, которая приходилась на одну акцию в момент учреждения компании.

Эмиссионная цена представляет собой цену, по которой акция эмитируется, т.е. продаётся на первичном рынке (это цена посреднической фирмы).

Балансовая стоимость – может быть рассчитана как отношение стоимости «чистых» активов (общая стоимость активов по балансу за минусом задолженности кредиторам) к общему числу выпущенных акций.

Ликвидационная стоимость может быть определена лишь в момент ликвидации общества. Она показывает, какая часть стоимости активов по ценам возможной реализации, оставшаяся после расчётов с кредиторами, приходится на одну акцию. Поскольку учётные цены активов могут значительно отличаться от их рыночных цен в зависимости от инфляции и конъюнктуры рынка, ликвидационная стоимость не равна балансовой.

Курсовая цена акции – цена на вторичном рынке ценных бумаг. Она может определяться различными способами, однако, в основе их лежит один и тот же принцип – сопоставление дохода, приносимого данной акцией, с рыночной нормой прибыли.

Оценка целесообразности приобретения акций предполагает расчёт теоретической стоимости акции и сравнение её с текущей рыночной ценой.

Привилегированные акции генерируют доход неопределённо долго, поэтому их текущая стоимость определяется по формуле (4.3).

Для оценки обыкновенных акций существуют различные методы, наиболее распространённый из них – метод, основанный на оценке их будущих поступлений по уравнению (4.1).

Оценка акций с равномерно возрастающими дивидендами производится по формуле Гардона:

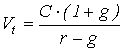,                                     (4.6)

где       C – базовая величина дивиденда (последнего выплаченного

                    дивиденда);

             g - темп прироста дивиденда;

             r – ожидаемая доходность.

Формула Гардона имеет смысл при r>g.

Из формулы (4.6) видно, что текущая цена обыкновенной акции очень чувствительна к параметру g, – даже незначительное его изменение может существенно повлиять на цену. Поэтому в расчётах пытаются разбить интервал прогнозирования на подинтервалы, каждый из которых характеризуется собственным темпом прироста g. Так, если выделить два подинтервала с темпами прироста g и р, то формула (4.1) примет вид:

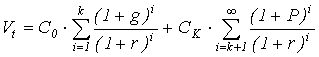.                       (4.7)

Главная сложность этой модели состоит в выделении подпериодов, прогнозировании темпов прироста и коэффициентов дисконтирования для каждого подпериода.

В теории и практике оценки акций описана и получила достаточно широкое распространение ситуация, когда темп прироста дивидендов в течении нескольких лет прогнозного периода меняется (фаза непостоянного роста), однако по истечении этих лет он устанавливается на некотором постоянном уровне. Считается, что такое развитие событий характерно для компаний, находящихся в стадии становления, либо уже зрелых компаний, осваивающих новые виды продукции или перспективные рынки сбыта.

Пусть продолжительность фазы непостоянного роста составляет k лет, дивиденды в этот период по годам равны C_j (j=1,2,…, k), С_k+1 – первый ожидаемый дивиденд фазы постоянного роста с темпом g.

Тогда на основании формулы (4.6) второе слагаемое в формуле (4.7) будет иметь вид:

.

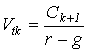Показатель V_tk даёт оценку акции на конец периода k. Поскольку делаем оценку акции с позиции начала первого года, значение V_tk нужно дисконтировать. Формула (4.7), позволяющая рассчитать теоретическую стоимость акции на конец «нулевого» года имеет вид:

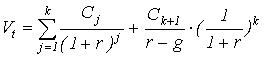,                                  (4.8)

Пример. В течении последующих четырёх лет компания планирует выплачивать дивиденды, соответственно, 1,5; 2; 2,2; 2,6 доллара на акцию. Ожидается, что в дальнейшем дивиденд будет увеличиваться равномерно с темпом роста 4% в год. Рассчитать теоретическую стоимость акции, если рыночная норма прибыли 12%.

Величина ожидаемого дивиденда пятого года будет равна 2,6*1,04=2,7 доллара. По уравнению (4.8):

 

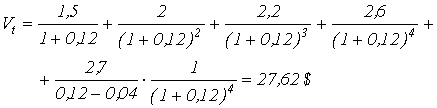
Доходность акций

Приобретая акции, инвестор вправе рассчитывать на два вида потенциальных доходов: а) дивиденд; б) доход от прироста капитала.

Общий доход, генерируемый инвестицией P₀, за данный период (t₀, t₁) составит величину:

,

а общая доходность (k_t) будет равна:

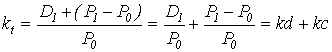,                    (4.9)

 

где             kd – дивидендная доходность;

                  kc – капитализированная доходность.

Доходность привилегированной бессрочной акции, равно как и обыкновенной акции, с неизменным дивидендом, определяется по уравнению:

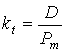,                                                  (4.10)

где             D – ожидаемый дивиденд;

                  P_m – текущая рыночная цена акции.

При принятии решения о целесообразности покупки акции на основе формулы (4.10) неявно считается, что инвестор не предполагает продать её в ближайшем будущем. Поэтому общая доходность здесь совпадает с текущей дивидендной доходностью. Такой оценки в принципе достаточно для принятия решения.

Если инвестор приобретает акцию в спекулятивных целях, намереваясь продать её через некоторое время, то он может получить некоторые оценки ожидаемых значений общей, дивидендной и капитализированной доходности. По аналогии с формулой (4.9):

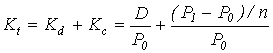,                                (4.11)

где         P₀ – рыночная цена акции в момент принятия решения о покупке;

             P₁ – ожидаемая цена акции на момент предполагаемой её продажи;

             n – ожидаемое число лет владения акцией.

Для оценки значения ожидаемой общей доходности обыкновенных акций с равномерно возрастающими дивидендами можно воспользоваться формулой полученной на основании модели Гардона (4.6):

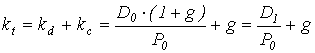,                         (4.12)

где      D₀ – последний полученный к моменту оценки дивиденд на акции;

           D₁ – ожидаемый дивиденд;

           P₀ – цена акции на момент оценки;

          g – темп прироста дивиденда.

IV.  Концепция риска и методы его оценки

Существуют различные определения понятия «риск». В наиболее общем виде под риском понимают вероятность возникновения убытков или недополучения доходов по сравнению с прогнозируемым вариантом. Риск может быть определён как уровень конкретной финансовой потери, выражающейся а) в возможности не достичь поставленной цели; б) неопределённости прогнозируемого результата; в) субъективности оценки прогнозируемого результата.

Риск является вероятностной оценкой, его количественное  измерение не может быть однозначным и предопределённым.

Количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода или доходности. Для количественной оценки риска можно использовать ряд статистических коэффициентов, в частности: размах вариации, дисперсию, среднее квадратичное отклонение и коэффициент вариации.

Размахом вариации называется разность между максимальным и минимальным значениями признака данного ряда:

.                                     (4.13)

Этот показатель имеет много недостатков, выделим лишь три из них:

1.     он даёт грубую оценку степени вариации значений признака;

2.     он является абсолютным показателем и поэтому его применение в сравнительном анализе весьма ограничено;

3.     его величина слишком зависит от крайних значений ранжированного ряда.

Дисперсия является средним квадратом отклонений значений признака от его средней величины и определяется по уравнению:

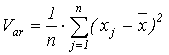,                             (4.14)

где                                .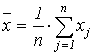

Среднее квадратичное отклонение показывает среднее отклонение значений варьирующего признака относительно центра распределения. Этот показатель определяется по формуле:

,                                                   (4.15).

Все вышеперечисленные показатели имеют один общий недостаток – это абсолютные показатели, значение которых существенно зависит от абсолютных значений исходного признака ряда. Исходя из этого, большое применение имеет коэффициент вариации (CV), определяемой по формуле:

,                                       (4.16)

В любом перспективном анализе инвестор сталкивается с одной проблемой, а именно с проблемой оценки ожидаемых значений исходных параметров. Какой бы мерой инвестор ни пользовался, ему необходимо оценить доходность актива. Чаще всего делают три оценки: пессимистическую (kp), наиболее вероятную (km) и оптимистическую (k₀).

Если ограничиваются тремя оценками, то наиболее общей мерой риска, ассоциируемого с данным активом, может служить размах вариации определяемой доходности:

.

Пример.

Предпринимателю необходимо выбрать лучший из двух альтернативных финансовых активов, если имеются следующие их характеристики:

Показатель	Вариант А	Вариант В
Цена ценной бумаги, тыс. руб.	12	18
Доходность (экспертная оценка), %
Пессимистическая	14	13
Наиболее вероятная	16	17
Оптимистическая	18	21
Размах вариации доходности, %	4	8

 

Из таблицы видно, что оба финансовых актива имеют примерно одинаковую вероятную доходность, однако второй из них считается в два раза более рисковым.

Можно рассчитать и другие меры риска, основанные на построении вероятностного распределения значений доходности и исчислении стандартного отклонения от средней доходности и коэффициента вариации, которые и рассматриваются как степень риска. Чем выше коэффициент вариации, тем  рисковым является данный вид актива. Последовательность аналитических процедур в этом случае такова:

-         делаются прогнозные оценки значений доходности (k_i) и вероятностей их осуществления (P_i), i = 1, 2, …, n – число исходов;

-         рассчитывается наиболее вероятная доходность (k_m) по уравнению:

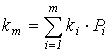                                               (4.17)

-         рассчитывается стандартное отклонение () по уравнению:

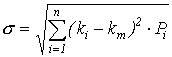,                                 (4.18)

-         рассчитывается коэффициент вариации (CV) по уравнению:

,                                                 (4.19)

Пример: В условиях предыдущего примера оценить риск каждого из альтернативных финансовых инструментов, если в обоих случаях вероятности наиболее возможной доходности 60%, а вероятности пессимистической и оптимистической оценок равны и составляют 20%.

Вариант А

Вариант В

Вариант В является более рискованным по сравнению с вариантом А.

V.  Риск инвестиционного портфеля

Чаще всего инвестор работает не с отдельным активом, а с некоторым их набором, называемым портфелем ценных бумаг, или инвестиционным портфелем.

Оценивая риск конкретного актива из инвестиционного портфеля, можно действовать двояко: либо рассматривать этот актив изолированно от других активов, либо считать его неотъемлемой частью портфеля. Оказывается, что оценка рискованности актива и целесообразности операции с ним могут меняться. Более того, актив, имеющий высокий уровень риска при рассмотрении его изолированно, может оказаться практически безрисковым с позиции портфеля – при определённом сочетании входящих в этот портфель активов. Например, теоретически можно подобрать два финансовых актива, каждый из которых имеет высокий уровень риска, но которые, будучи объединенными вместе, составят абсолютно безрисковый портфель.

При оценке портфеля и целесообразности операций с входящими в него активами, необходимо оперировать показателями доходности и риска портфеля в целом.

Доходность портфеля (k_p) представляет собой линейную функцию показателей доходности входящих в него активов и может быть рассчитана по формуле средней арифметической взвешенной (в данном случае речь может идти как об ожидаемой, так и о фактической доходности):

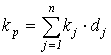,                                   (4.20)

где    k_j – доходность j-го актива;

          d_j – доля j-го актива в портфеле;

          n – число активов в портфеле.

Как и в случае с отдельными активами, мерой риска портфеля служит вариация его доходности, взаимосвязь между риском портфеля и риском входящих в него активов носит более сложный характер и не описывается формулой средней арифметической.

В частности, если в качестве меры риска выбрано среднее квадратическое отклонение, то его значение для портфеля, содержащего k активов, может быть определено по уравнению:

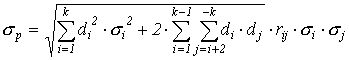,          (4.21)

где    d_i – доля i-го актива в портфеле;

          _i – вариация доходности i-го актива;

          r_ij – коэффициент корреляции между ожидаемыми доходностями i-го и j-го активов.

Ситуация осложняется при переходе к портфелям с большим числом входящих в них активов. В этом случае возникает ряд проблем как теоретического, так и вычислительного характера.

Во-первых, в ситуации с портфелем риск, ассоциированный с каким-то конкретным активом, не может рассматриваться изолированно.

Во-вторых, поскольку, все финансовые инвестиции различаются по уровню доходности и риска, их возможные сочетания в портфеле усредняют эти количественные характеристики, а в случае оптимального их сочетания можно добиться значительного снижения риска финансового инвестиционного портфеля.

В-третьих, приемлемая доходность не может быть достигнута простым отбором наиболее доходных активов, поскольку обычно приводит к увеличению риска портфеля.

В-четвёртых, вариация доходности имеет место не только в пространстве, но и динамике, т.е. тенденции доходности двух случайно выбранных из портфеля активов вовсе не обязательно совпадают, более того, они могут быть разнонаправленными.

В-пятых, в условиях множественности входящих в портфель активов существенно усложняются вычислительные процедуры.

Вопросы для контроля

1.     Основные теории оценки ценных бумаг?

2.     Способы выплат доходов по облигациям?

3.     Стоимостные показатели облигаций?

4.     Доходность акций?

5.     Концепция риска и методы его оценки?

6.     Риск инвестиционного портфеля?