Глава I.
Теоретические основы, классификация
приёмов и способов экономического анализа
I. Теоретические основы экономического анализа
Анализ
– означает разложение изучаемого объекта на части, на присущие этому объекту
составляющие. Анализ выступает в диалектическом, противоречивом единстве с понятием
синтез – соединение ранее расчленённых элементов изучаемого объекта в единое
целое. Диалектический тандем анализ – синтез понимается как синоним всякого
научного исследования.
Особое
значение анализ и синтез приобрели в экономике. Анализом в более широком смысле
занимается теория экономического анализа; в профессиональном – экономический
анализ финансово-хозяйственной деятельности в соответствующих отраслях промышленности,
сельском хозяйстве, строительстве, торговле и т.д.
Содержанием
и предметом экономического анализа определяются стоящие перед ним задачи. Важнейшие
из них:
- повышение научно-экономической
обоснованности бизнес-планов, бизнес процессов и нормативов (в процессе их
разработки);
- объективное и всестороннее изучение по
данным учёта и отчётности выполнения установленных бизнес-планов, бизнес
процессов и соблюдения нормативов по количеству, структуре и качеству
выпущенной продукции, выполненных работ и услуг;
- определение экономической эффективности
использования трудовых, материальных и финансовых ресурсов;
- обеспечение заданной эффективности и оценка
конечных финансовых результатов;
- выявление и измерение внутренних резервов на
всех стадиях производственного процесса;
- в обосновании и проверке оптимальности
управленческих решений.
Совокупность
приёмов и способов, которые применяются при изучении хозяйственных процессов,
составляют методику экономического анализа. Методика анализа имеет свои
особенности на различных этапах исследования:
- при первичной обработке информации;
- для изучения состояния и закономерностей
развития исследуемых объектов;
- при определении влияния факторов на
результаты деятельности предприятий;
- для оценки резервов роста эффективности
производства;
- при обосновании бизнес-планов.
На каждом
этапе применяется определённый перечень аналитических приёмов и способов. Так,
при первичной обработке информации применяются методы группировки показателей,
сравнение, графическое представление анализируемой информации, расчёт относительных
и средних величин.
Изучение
состояния и закономерностей развития исследуемых объектов осуществляется с
помощью статистических методов анализа показателей рядов динамики.
С целью
определения влияния факторов на результаты деятельности предприятий
используется множество приёмов и способов, составляющих содержание факторного
анализа.
В оценке
резервов и обосновании бизнес-плана распространены методы: экономические,
матричные, теории производственных функций, теории межотраслевого баланса, оптимального
программирования.
Экономический
анализ – это прежде всего факторный анализ.
Под
экономическим факторным анализом понимается постепенный переход от исходной
факторной системы к конечной факторной системе, раскрытие полного набора
прямых, количественно измеряемых факторов, оказывающих влияние на измерение
результативного показателя.

Рис.
1.1 методы факторного анализа
По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа.
Функционально - детерминированная связь – это связь, при которой каждому значению факторного признака соответствует вполне определённое неслучайное значение результативного признака. Связь, при которой каждому значению факторного признака соответствует множество значений результативного признака (т.е. определённое статистическое распределение) – стохастическая (вероятностная) связь. Соответственно типу связи аналитические приёмы и способы делятся на методы детерминированного факторного анализа и методы стохастического факторного анализа (рис. 1.1).
II. Детерминированный факторный анализ
2.1 . Модели
детерминированного факторного анализа.
Детерминированный факторный анализ представляет собой методику
исследования влияния факторов, связь которых с результативным показателем носит
функциональный характер, т.е. может быть выражен математической зависимостью. Детерминированные модели могут быть разного типа:
аддитивные, мультипликативные, кратные, смешанные.
2.1.1
Аддитивные модели
Аддитивные модели представляют собой алгебраическую сумму показателей и имеют следующую математическую интерпретацию:
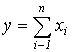
В качестве
примера можно привести балансовую модель товарного обеспечения: ![]()
где Np – общий объём реализации;
Nзап.1 – запасы товара на начало периода;
Nn – объём поступления;
Nвыб – прочее выбытие товаров;
Nзап.2 – запасы товаров на конец анализируемого периода.
2.1.2 Мультипликативная модель
Мультипликативная
модель представляет собой
произведение факторов. 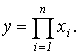
Примером
мультипликативной модели является двухфакторная модель объёма реализации: ![]()
где Ч – среднесписочная численность работников;
В – выработка на одного работника.
2.1.3 Кратные модели
Кратные
модели представляют собой отношение факторов и имеют вид:
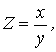
где Z – совокупный показатель.
Например: 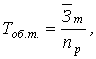
где ![]() – срок оборачиваемости
товаров (в днях);
– срок оборачиваемости
товаров (в днях);
![]() - средний запас
товаров;
- средний запас
товаров;
nр – однодневный объём реализации.
2.1.4 Смешанные модели
Смешанные модели представляют собой комбинацию перечисленных моделей. Примером смешанной модели является формула расчёта интегрального показателя рентабельности

где Rк – рентабельность капитала;
Rnp – рентабельность продаж;
Fe – фондоёмкость основных средств;
Eз – коэффициент закрепления оборотных средств.
2.2 Способы оценки влияния факторов
в
детерминированном факторном анализе
Задача детерминированного факторного анализа заключается в определении или количественной оценке влияния каждого фактора на результативный показатель. Способы детерминированного факторного анализа представлены на рис. 1.1
Наиболее часто применяется способ цепных подстановок, основанный, как и ряд других, на элиминировании. Элиминировать – это значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного.
Количество расчётов может быть несколько сокращено, если использовать модификацию способа цепных подстановок – способ разниц.
Изменение результативного показателя за счёт каждого фактора способом разниц определяется как произведение отклонения изучаемого фактора на базисное или отчётное значение другого (других) факторов в зависимости от выбранной последовательности подстановки.
2.2.1
Логарифмический способ
Логарифмический способ применим к кратным и мультипликативным моделям. Он основан на логарифмировании отклонения отчётного и базисного значений результативного признака, равного отношению соответствующих произведений факторов, так как изменение показателей может быть оценено с помощью как абсолютных, так и относительных показателей.
2.2.2
Способ долевого участия.
Способ долевого участия. Этот способ заключается в определении доли каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост совокупного показателя. Этот метод применяется к аддитивным моделям и чаще всего для оценки влияния факторов второго или третьего порядков.
Для примера рассмотрим модель зависимости фонда заработной платы от средней заработной платы и численности персонала.
![]() (1.1)
(1.1)
где ФЗ – фонд заработной платы;
ЗП – средняя заработная плата;
Ч - среднесписочная численность.
В свою очередь средняя заработная плата равна сумме средних выплат по тарифным ставкам, доплат, надбавок (ДН) и дополнительной заработной платы (ДЗ).
Модель примет вид:
![]()
Пользуясь способом разниц, рассчитаем влияние средней заработной платы и численности персонала на изменение фонда заработной платы по данным таблицы 1.1

Итого: 68400 руб.
Данные для расчёта
Таблица 1.1
|
Показатель |
Базисный
период |
Отчётный
период |
Отклонения |
|
Фонд
заработной платы, руб. в
том числе по
тарифным ставкам доплаты,
надбавки дополнительная
зарплата |
240000 172000 44000 24000 |
308000 189000 81000 38000 |
+68000 +17000 +37000 14000 |
|
Среднесписочная
численность, человек |
15 |
16 |
+1 |
|
Среднегодовая
заработная плата, руб. том
числе тарифные
ставки (ТС) доплаты,
надбавки (ДН) дополнительная
заработная плата (ДЗ) |
16000 11467 2933 1600 |
19250 11813 5062 2375 |
+3250 +346 +2129 +775 |
Для определения влияния каждого вида выплат на изменение фонда заработной платы рассчитаем долю (D) влияния каждого вида выплат на среднюю заработную плату:
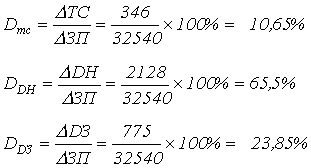
Влияние каждого вида выплат на фонд заработной платы составит:
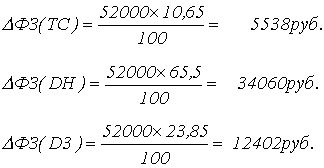
Итого: 52000 руб.
Сведём
полученные результаты в таблицу 1.2![]()
.
Влияние факторов на фонд заработной платы
Таблица 1.2
|
Фактор |
Размер влияния, руб. |
Доля влияния на фонд
заработной платы, % |
Доля влияния на среднюю
заработную плату, % |
|
Среднесписочная численность |
16000 |
23,5 |
|
|
Средняя заработная плата, В том числе: по тарифным ставкам выплаты, надбавки Дополнительная заработная
плата |
52000 5538 34060 12402 |
76,5 |
10,65 65,5 23,85 |
|
Итого |
68000 |
100 |
100 |
Проведённый расчёт показывает, что увеличение фонда заработной платы на 23,5% вызвано ростом среднесписочной численности персонала и на 76,5% - изменением средней заработной платы.
2.2.3
Индексный метод
Индексный метод основан на построении факторных (агрегированных) индексов. Применение агрегированных индексов означает последовательное элиминирование влияния отдельных факторов на совокупный показатель. Преимущество индексного метода заключается в том, что он позволяет произвести «разложение» по факторам не только абсолютное изменение показателя, но и относительное, что особенно важно при изучении факторных динамических моделей.
Так, индекс изменения выпуска продукции можно выразить через произведение индексов численности и выработки:
![]()
С помощью индексного метода можно определить влияние факторов, в том числе структурных сдвигов, на абсолютное отклонение результативного показателя.
Индексный метод целесообразно применять в том случае, когда каждый фактор является сложным (совокупным) показателем. Например, численность персонала предприятия представляет собой соотношение численности отдельных категорий работников или рабочих различных разрядов. Изменение объёма выпуска продукции происходит не только под влиянием численности и выработки, но и структурных сдвигов в составе персонала.
2.2.4
Интегральный способ
Интегральный способ позволяет достичь полного разложения результативного показателя по факторам и носит универсальный характер, т.е. применим к мультипликативным, кратным и смешанным моделям.
Операция вычисления определённого интеграла по заданной подынтегральной функции и заданному интервалу интегрирования выполняется на ПЭВМ.
III. Корреляционно-регрессивный
анализ
Если связь между показателем не является строго детерминированной, то она корреляционная. Она характеризуется тем, что, помимо изучаемых условных факторов, на результативный показатель оказывают влияние и побочные факторы, искажающие влияние основного.
Обязательным условием применения корреляционного метода является массовость значений изучаемых показателей, позволяющая выявить тенденцию, закономерность развития.
Корреляция может быть парной и множественной.
Парная корреляция – это связь между двумя показателями, один из которых является фактором, другой – результативным показателем.
Множественная корреляция – связь между несколькими факторами и одним результативным показателем.
Алгоритм расчёта при корреляционном анализе связи парной корреляции состоит из ряда этапов.
Этап 1. Производится отбор наиболее важных существенных факторов, влияющих на результативный показатель. При отборе факторов учитываются причинно-следственные связи между показателями, причём все факторы должны быть количественно измеримы.
Этап 2. Данные из таблицы наносятся на плоскость координат – строится корреляционное поле.
Этап 3. Производится обоснование формы связи:
- по форме корреляционного поля;
- путём визуального анализа ранжирования ряда.
Этап 4. Выбор и решение уравнения регрессии осуществляется с применением ПЭВМ.
Метод множественной корреляции применяется в случаях, когда результирующий показатель зависит от нескольких взаимно независимых факторов. При этом применяется уравнение множественной регрессии.
![]() (1.2)
(1.2)
IV.
Матричный
метод и его применение
в сравнительном многомерном анализе
Матричные методы анализа основаны на линейной и векторно-матричной алгебре и применяются для изучения сложных и многомерных структур. Сферы применения матричного метода экономического анализа многообразны, но наиболее широкое распространение получил метод для сравнительной оценки деятельности различных систем (предприятий, структурных подразделений и т.п.).
Алгоритм расчёта матричного метода состоит из нескольких этапов:
Этап 1. Обоснование системы оценочных показателей и формирование матрицы исходных данных aij, т.е. таблицы, где по строкам отражаются номера систем (i = 1, 2,…, n), а по столбцам – номера показателей (j = 1, 2, ,m).
Этап 2. В каждом столбце определяется максимальный элемент, который принимается за единицы. Затем, все элементы этого столбца aij делятся на максимальный элемент, и создаётся матрица стандартизованных коэффициентов xij.
Этап 3. Все элементы матрицы возводятся в квадрат. Если значимость показателей, составляющих матрицу, различна, тогда каждому показателю присваивается весовой коэффициент k, который определяется экспертным путём.
Рейтинговая оценка по каждой системе определяется по формуле:
![]() (1.3)
(1.3)
Этап 4. Полученные рейтинговые оценки Rj размещаются в порядке убывания или возрастания в зависимости от экономического смысла показателей, составляющих рейтинг.
Результаты сравнительного анализа могут применяться для определения инвестиционной привлекательности партнёра.
Этап 1
Матрица исходных данных.
Таблица 1.3
|
Номера исследуемых систем |
Рентабельность капитала |
Оборачиваемость капитала |
Коэффициент тенденций
ликвидности |
Коэффициент автономности |
Доля собственных. средств
в обороте |
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
5,6 |
7,2 |
1,7 |
0,65 |
0,1 |
|
2 |
4,1 |
9,5 |
0,6 |
0,45 |
0,15 |
|
3 |
6,2 |
4,1 |
1,9 |
0,54 |
0,28 |
|
4 |
7,8 |
8,2 |
2,0 |
0,72 |
0,22 |
|
5 |
6,5 |
6,4 |
2,2 |
0,68 |
0,14 |
Этап 2
Матрица стандартизированных коэффициентов. Таблица 1.4
|
Номера исследуемых систем |
Показатели |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0,718 |
0,758 |
0,773 |
0,903 |
0,036 |
|
2 |
0,525 |
1 |
0,273 |
0,625 |
0,536 |
|
3 |
0,795 |
0,432 |
0,864 |
0,750 |
1 |
|
4 |
1 |
0,863 |
0,909 |
1 |
0,786 |
|
5 |
0,833 |
0,674 |
1 |
0,944 |
0,500 |
Значимость коэффициентов предполагается одинаковой, поэтому достаточно их возвести в квадрат, сложить по строкам и по уравнению (1.3) определить рейтинговую оценку.
Система 4 имеет самую высокую рейтинговую оценку.
Рассмотренные
методы экономического анализа имеют практическую значимость и могут быть
применены для оценки любого показателя или сферы деятельности предприятия, чаще
всего в комплексе.
Матрица квадратов и рейтинговая оценка
исследуемой системы
Таблица 1.5
|
Номера исследуемых систем |
Показатели |
Ri |
Место |
||||
|
1 |
2 |
3 |
4 |
5 |
|
||
|
1 |
0,516 |
0,575 |
0,598 |
0,815 |
0,001 |
1,300 |
V |
|
2 |
0,277 |
1 |
0,075 |
0,391 |
0,287 |
1,425 |
IV |
|
3 |
0,632 |
0,187 |
0,746 |
0,563 |
1 |
1,769 |
III |
|
4 |
1 |
0,745 |
0,826 |
1 |
0,618 |
2,047 |
I |
|
5 |
0,694 |
0,454 |
1 |
0,891 |
0,250 |
1,814 |
II |
Вопросы для контроля
1. Какие принципы лежат в основе классификации приёмов и способов финансово - экономического анализа?
2. Чем отличаются способы детерминированного и стохастического факторного анализа?
3. Способы построения детерминированных факторных моделей?
4. Простые способы детерминированного факторного анализа (способ цепных постановок, способ разниц)?
5. Применение матричного метода в сравнительном многомерном анализе?